Goals
Upon successful completion of this lab, you should be able to understand and write functions using two-dimensional (nested) lists.
Setup and Practice
Setup
- If your lab machine was not started in MacOS when you went to use it, reboot it to MacOS.
- Follow these procedures to mount your blue home-directory on the local machine and create a PyCharm project (call it Lab08). You will use PyCharm in the next part, but, it is important that you set up your project now so that if you run into any issue, we can resolve them quickly.
- Right-click or control-click to download these 4 files and place them into the directory for this lab:
Practice: Creating and accessing 2D lists
At this point, you should be very comfortable using and manipulating one-dimensional lists. Lists usually are created and accessed through loops. For example, this code creates a list of 10 elements, where each element has a value of 0:
my_list = [] # create an empty list
for i in range(10):
my_list.append(0)
We can also create and initialize a list in a single statement:
list_of_values = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
The elements of a list can be of any data type, including other lists. For example:
two_three = [ [1, 2, 3], [10, 11, 13] ]
Here, we have a list with two elements. Each of the elements is itself a list, which makes two_three a two-dimensional list. Each of the elements of two_three can be called a row, and each row has three elements (columns).
Copy and paste the following code into the online Python 3 tutor, run it one step at a time, and answer Question 1 in your writeup.
two_three = [ [1, 2, 3], [10, 11, 13] ] for i in range(2): # Two rows for j in range(3): # Three columns print(two_three[i][j], ' ', end='') print()-
Using a new browser tab, run the following code in the Python Tutor, and compare it with the previous example. Then answer Question 2 in your writeup.
two_three = [ [1, 2, 3], [10, 11, 13] ] num_rows = len(two_three) for i in range(num_rows): list_i = two_three[i] # The i-th element of two_three num_columns = len(list_i) for j in range(num_columns): print(list_i[j], ' ', end='') print() -
Here is yet another code segment that does exactly the same thing. Using a new browser tab, copy and paste it in Python Tutor and run through it one step at a time. Then answer Question 3 in your writeup.
def print_list(list_to_print): for i in range(len(list_to_print)): print(list_to_print[i], ' ', end='') print() def print_2d_list(two_d_list): for i in range(len(two_d_list)): print_list(two_d_list[i]) def main(): two_three = [ [1, 2, 3], [10, 11, 13] ] print_2d_list(two_three) main()
Practice: building 2D lists with append
Copy and paste the following code into the online Python 3 tutor, run it one step at a time
v = 0 two_d = [] # create an empty list for i in range(5): two_d.append([]) # append an empty list to two_d for j in range(4): two_d[i].append(v) # two_d[i] is the empty list that we just created. # here, we are adding elements to it. v += 1- Answer Question 4 in your writeup.
Part A: Create a magic square
A magic square is an N by N matrix whose elements contain the values 1 through N2, and where the sums of the values in each row, column, and diagonal are equal. Here is an example of a 5x5 magic square.
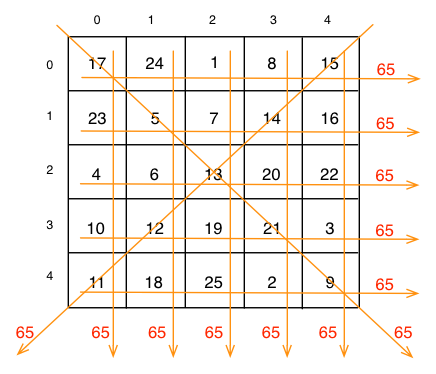
There is a simple algorithm for creating magic squares with odd values of N, like the example one above. You will see that algorithm shortly and will use it to write a program that both creates a magic square and verifies that what it creates is indeed a magic square.
Instructions
Create a new Python file called lab08a.py:
""" Program: CS 115 Lab 8a Author: Your name Description: This program will create a magic square whose size is specified by the user. """ def create_list(rows, cols): '''Creates a two-dimensional array. Args: rows (int): The numbers of rows. cols (int): The number of columns. Returns: list: A 2D array with all values set to zero. ''' two_d = [] # create an empty list for i in range(rows): two_d.append([]) # append an empty list to two_d for j in range(cols): two_d[i].append(0) # two_d[i] is the empty list that we just created. # here, we are adding elements to it. return two_d def rjust_by_n(number, n): '''Formats a string containing 'number', right-justified. Args: number (int): A value. n (int): The width of the string into which 'number' is inserted. Returns: str: A string of length n. ''' return str(number).rjust(n) def print_list(numbers): '''Prints a 1D list of numbers, where each number is right-justified. Args: numbers (list): A list of numbers. ''' for i in range(len(numbers)): print( rjust_by_n(numbers[i], 4), end='') print() def print_2d_list(two_d_list): '''Prints a 2-dimensional list in a pretty format. Args: two_d_list (list): A 2D list of numbers. ''' for i in range(len(two_d_list)): print_list(two_d_list[i]) def main(): # TODO: your code goes here main()- Read through the provided functions --- you will need to call some of them later.
In
main, ask the user to enter an integer to be used to create a magic square, and save that integer into a variablesquare_size.Sample input/output:
Enter an odd integer to build a magic square: 5
Make sure that the user's input (
square_size) is odd. If it is not, print an error message and exit, or return frommain:Enter an odd integer to build a magic square: 6 6 is not an odd integer. Terminating...
If the input integer is odd, create a matrix (a two dimensional list) of that size and print it by right-justifying each value in exactly 4 spaces. Use the provided functions to help with this task. Creating the list should take 1 line of code, printing the blank line should take another, and printing the matrix should take 1 more.
Enter an odd integer to build a magic square: 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Copy and paste the following function in your program.
def build_magic_square(square): '''Modifies 'square' to fill it with a magic square. Modifies the original list (has no return value). Args: square (list): a 2D array whose number of rows and columns are equal and len(square) is an odd number. ''' magic_value = 1 square_size = len(square) row = 0 col = square_size // 2 square_size_squared = square_size * square_size while magic_value <= square_size_squared: square[row][col] = magic_value row -= 1 col += 1 if row < 0 and col > square_size - 1: row += 2 col -= 1 elif row < 0: row = square_size - 1 elif col > square_size - 1: col = 0 elif square[row][col] != 0: row += 2 col -= 1 magic_value += 1In
main, insert a call to this function to build a magic square. This function call should go in between the lines of code that create and print the 2D list.Sample input/output:
Enter an odd integer to build a magic square: 5 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9
Another example:
Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20
- Continue to Part B.
Part B: Verify magic squares
In this part of the lab, you will make sure that your magic square really is a magic square by calculating the sums of the numbers in each row, column, and diagonal.
In order to test your code, you'll also call a function to read magic squares from a user-specified file.
Instructions
- Make a copy of your lab08a.py file, naming the copy lab08b.py.
- You'll start by writing a function to calculate the sum of all values in a given row of this matrix. First, answer Question 5 in your writeup.
- Using what you learned, complete this function definition.
def sum_row_values(matrix, row_number): '''Sums the values of all entries in the row given by 'row_number'. Args: matrix (list): A square, 2D array. row_number (int): A value in the range 0 and len(matrix)-1. Returns int: The sum of all values of the row indicated by 'row_number'. ''' # TODO: Your code goes here You can test this code by adding the following lines to the end of main. Substitute your own magic square variable where highlighted:
sum_of_row_0 = sum_row_values(your variable, 0) print() print('The sum of values in row 0 is', sum_of_row_0)The output should look like this:
Enter an odd integer to build a magic square: 5 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 The sum of values in row 0 is 65
Here is another example:
Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20 The sum of values in row 0 is 175
Now modify your main function to print the sum of each row. Sample input/output:
Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20 The sum of values in row 0 is 175 The sum of values in row 1 is 175 The sum of values in row 2 is 175 The sum of values in row 3 is 175 The sum of values in row 4 is 175 The sum of values in row 5 is 175 The sum of values in row 6 is 175
- Next, you'll write a function to sum the values in a given column. Answer Question 6 in your writeup.
Using what you learned, complete this function definition.
def sum_col_values(matrix, col_number): '''Sums the values of all entries in the column given by 'col_number'. Args: matrix (list): A 2D, square array. col_number (int): A value in the range 0 and len(matrix)-1. Returns: int: The sum of all values in the column indicated by 'col_number'. ''' # TODO: Your code goes hereIn main, call your new function:
Enter an odd integer to build a magic square: 5 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9 The sum of values in column 0 is 65 The sum of values in column 1 is 65 The sum of values in column 2 is 65 The sum of values in column 3 is 65 The sum of values in column 4 is 65
Another example:
Enter an odd integer to build a magic square: 9 47 58 69 80 1 12 23 34 45 57 68 79 9 11 22 33 44 46 67 78 8 10 21 32 43 54 56 77 7 18 20 31 42 53 55 66 6 17 19 30 41 52 63 65 76 16 27 29 40 51 62 64 75 5 26 28 39 50 61 72 74 4 15 36 38 49 60 71 73 3 14 25 37 48 59 70 81 2 13 24 35 The sum of values in column 0 is 369 The sum of values in column 1 is 369 The sum of values in column 2 is 369 The sum of values in column 3 is 369 The sum of values in column 4 is 369 The sum of values in column 5 is 369 The sum of values in column 6 is 369 The sum of values in column 7 is 369 The sum of values in column 8 is 369
We are ready to calculate the sum of the diagonals. Let's start with the top-left to the bottom-right diagonal. For a 3x3 matrix, the indices of these values are (0, 0), (1, 1), (2, 2). Write a function to calculate the sum of values on this diagonal, based on the below definition.
def sum_top_left_bottom_right_diagonal(matrix): '''Calculates the sum of the values at matrix[0][0], matrix[1][1], etc. Args: matrix (list): A square, 2D array. Returns: int: The sum of values of the top-left to bottom-right diagonal. '''Add code to
mainto test this function before you proceed.- Write a function to sum the value of the top-right to bottom-left diagonal, based on the below definition. For a 3x3 matrix, the indices of these values are: (0, 2), (1, 1), (2, 0).
def sum_top_right_bottom_left_diagonal(matrix): '''Calculates the sum of the values at matrix[0][len(matrix)-1], matrix[1][len(matrix)-2], etc. Args: matrix (list): A square, 2D array. Returns: int: The sum of values of the top-right to bottom-left diagonal '''This diagonal is harder than the previous one, but if you carefully study the indices of this diagonal of a few of the matrices above, you should see the pattern. Test this function before you proceed.
- Now you have everything you need to determine whether or not a given matrix
is a magic square. Complete the function definition below.
def is_magic_square(matrix): '''Returns True if the two dimensional array 'matrix' is a magic square; otherwise, returns False. Args: matrix (list): A square, 2D array. Returns: bool: True or False. ''' # TODO: Complete the below code # Calculate the sum of the values of the top-left to # bottom-right diagonal. Call it tlbr_sum. # Calculate the sum of the values of the top-right to # bottom-left diagonal. Call it trbl_sum. # If tlbr_sum is not equal to trbl_sum, return False. # Otherwise, proceed. # Calculate the sum of each row of the matrix and compare it # with tlbr_sum. If the two sums are not equal, return False. # Otherwise, proceed. # Calculate the sum of each column of the matrix and compare it # with tlbr_sum. If the two sums are not equal, return False. # Otherwise, proceed. # return True. - Test the entire program:
Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20 The above square is a magic square.
Add some code that will print
The above square is NOT a magic square.
if the sum of rows, the sum of columns, and sum of diagonals are not all equal.The
build_magic_squarefunction always returns valid magic squares. To make sure that your code actually works, you'll need to test it on some values that are not magic squares. You will read these from the files you downloaded during Setup at the beginning of the lab.Start by copying this function definition into your code:
def read_magic_square(filename): '''Reads values from a file into a 2D list. Args: filename (str): The name of the file. Returns: list: A 2D list of integer values. ''' infile = open(filename, 'rt') square = [] # start with an empty list for line in infile: # read text from file row = [] numbers = line.split() # Loop through the list of numbers. # Append each number to the row. for num in numbers: row.append(num) if len(row) > 0: # Don't count blank lines square.append(row) # Append the row to the 2D list return squareIn your
mainprogram, prompt the user for a filename after you have verified the original square. Sample output:Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20 The above square is a magic square. Enter the name of a file containing a matrix of numbers: ms1.txt
Pass the filename to
read_magic_squareto create a magic square. Print the resulting magic square just like you did for the first one. Sample output:Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20 The above square is a magic square. Enter the name of a file containing a matrix of numbers: ms1.txt 1 2 3 4 5 6 7 8 9
Now call your function to verify the new magic square. It should crash with an error message that ends like this:
TypeError: unsupported operand type(s) for +=: 'int' and 'str'
Fix yourread_magic_squarefunction to eliminate this error by making sure that the elements of your list are all integers. You should only need to change one line.- Test your program on all of the provided text files (ms1.txt through ms4.txt). Of these files, only ms4.txt should be reported as a valid magic square.
- Sample output:
Enter an odd integer to build a magic square: 7 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20 The above square is a magic square. Enter the name of a file containing a matrix of numbers: ms1.txt 1 2 3 4 5 6 7 8 9 The above square is NOT a magic square.
- If you look back at the definition of magic square in Part A, there is one property of a magic square that we are not checking for. Answer Question 7 in your writeup.
- Make sure that the docstring includes your name, the assignment number, and a description of the current version of your program.
- Demo. When your code is working, call an instructor over to demo.
- Continue to the next part to submit your program.
Assignment Submission
Instructions
- Answer the last question (#8) in your Moodle writeup. Review your answers, and then click the "Next" button at the bottom of the quiz. Once you do that, you should see a "Summary of Attempt" screen.
- Click the "Submit all and finish" button.
Warning: You must hit "Submit all and finish" so that your writeup can be graded! It is not submitted until you do this.
Once you have submitted your quiz, you should see something similar to this at the top of your Moodle window. The important part is that the State shows up as Finished.
Please leave this tab open in your browser. - Click on the "Lab 8 code" link in Moodle and open in a new tab. Follow the instructions to upload your source code (lab08b.py) for Lab08. You could either browse for your code or, using a finder window, drag and drop your lab08b.py from your cs115/Lab08 folder to Moodle. You should subsequently see a dialog box which indicates 'Submission Status' as 'Submitted for grading'. Leave this tab open in your browser.
- With these confirmation pages open in your browser, you may call an instructor over to verify that you have completed every part of the lab. Otherwise, you are done!